Glass T&am: Research Activity
HOME	RESEARCH		PUBLICATIONS	TEACHING	LINKS & MORE
The scientific activity of Mauro Corrado concerns different research areas ranging from Mechanics of Solids, to Fracture Mechanics, Computational Mechanics and Structural Design. The unifying aspect of the different topics is their connection with practical problems usually encountered in the design of concrete structures and composite materials with interfaces.
Research Topics
		• Structural Glass This is the most recent and, currently, the most representative research activity carried out within GLASS TEAM. Interests in this field include: (i) the improvement of the mechanical performances of glass by means of the use of functional coatings. Examples are the development of a coating able to inhibit stress corrosion, thus allowing the full exploitation of the tensile strength of glass, and a coating with tailored mechanical properties to reduce contact stress concentrations along the edges. (ii) the study of innovative structural systems with optimized mechanical and physical properties, such as, for instance, sandwich panels with excellent mechanical and thermal properties. Experimental research as well as multi-physics coupled analysis are carried out.
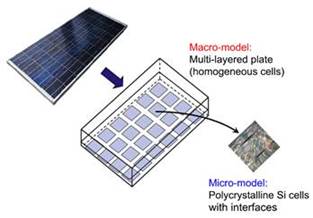
		• Multi-scale and multi-physics analysis Since 2012, Dr. Corrado is actively working on the multi-physics and multi-scale computational modelling of the evolution of microcracking in mono- and multi-crystalline Silicon (Si) solar cells embedded in photovoltaic (PV) modules. The aim is to develop a multi-scale nonlinear finite element approach to couple the structural scale of the PV laminate (macro-model) to the scale of the Si cell (micro-model). Inter-granular and trans-granular cracking in the Si cell is simulated using a nonlinear fracture mechanics cohesive zone model. The proposed approach permits to analyse the microcrack orientation and distribution, as well as the effect of cracking on the electric performance of the PV module. In particular, coupling between elastic and electric fields is proposed according to a one-diode electric model improved to include localized resistances due to the presence of cracks crossing Si cells. Experimental studies are also carried out to analyse the evolution of the crack pattern and of the electric performance (by means of the electroluminescence technique) in semi-flexible modules subjected to fatigue cycles, impact loads, and thermal loads.
		• Multi-scale FE approach to model failure in structural concrete Since September 2014, Dr. Corrado is working on the project “A multi-scale numerical approach for a consistent understanding and modelling of structural concrete”, related to the Marie Curie Fellowship recently awarded to him. The purpose of this project is to contribute to a consistent understanding and modelling of the complex cracking pattern, the interaction between steel rebars and concrete, and the behaviour of the compressed zone that lead to the final shear and punching collapse of reinforced concrete beams and slabs. Due to the wide kaleidoscope of sizes of the ingredients, concrete is modelled with a meso-mechanical approach in which aggregates and matrix are explicitly represented. Then, another challenging approach is the transfer of the meso-scale information to the engineering scale, by means of a multi-scale computational approach. An innovative aspect is to create a synergy between the simplified mechanical approach behind the development of standards and the most advanced computational mechanics ones, aiming at the improvement of the Standards.
		• Constitutive models for quasi-brittle materials This research concerns the analysis of the nonlinear softening behaviour of quasi-brittle materials (concrete, fibre-reinforced concrete, mortar, rocks) subjected to quasi-static uniaxial compression. Based on the hypothesis of strain localization in the post-peak regime, well supported by several experimental results available in the literature, a new constitutive model was proposed, the so-called Overlapping Crack Model (OCM). The main novelty is the introduction of a fictitious interpenetration describing the material damage occurring in the post-peak behaviour, that, in this way, is considered fully localized along a single band, whereas the bulk of the material exhibits a linear-elastic behaviour. The result is that the softening law obtained for a specific material, defined in terms of stress vs. fictitious interpenetration is scale-invariant. The application of the OCM to uniaxial compressive tests have permitted to analytically describe the overall response of a large number of compression tests available in the literature, correctly predicting complex phenomena such as size effects and ductile-to-brittle transitions (including snap-back instabilities). Its extension to fractal geometry, by considering that the energy dissipation and the strain localization take place in domains having non-integer physical dimensions, represents a further step toward the definition of scale-invariant constitutive laws for heterogeneous materials. Besides, the definition of such a fractal OCM has permitted to quantify the energy dissipated in the crushing process and the physical dimension of the damage domain for concrete and rock materials. In this research the applicant has acquired skills in nonlinear modelling of quasi-brittle materials.
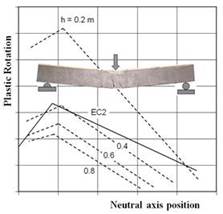
		• Ductility of reinforced concrete structural elements The present topic is relevant with respect to the very actual scientific debate concerning structural safety. A large plastic rotational capacity, in fact, concurs to withstand cyclic loadings due to earthquake actions, to redistribute the bending moment within statically indeterminate structures and to provide robustness. The main purpose of this research is the analysis of the ductility of reinforced concrete members in bending, with particular regard to the issue of size effects. To this aim, the cohesive and the overlapping crack models have been implemented into a numerical algorithm, together with a suitable nonlinear constitutive law for the steel reinforcement, in order to describe the cracking, crushing and yielding processes characterising the onset and the development of plastic hinges in reinforced concrete elements. The proposed algorithm has been validated by comparing the bending moment vs. rotation diagrams obtained by the numerical simulations with several experimental results available in the literature. Relevant results concerned the analysis of the size effects on the rotational capacity of plastic hinges and on the bending moment redistribution in statically indeterminate beam systems; the assessment of the minimum reinforcement amount necessary to avoid unstable crack propagation in tension; and the analysis of the size effects on the load-carrying capacity of plain and reinforced concrete elements eccentrically loaded. In these contexts, the application of Dimensional Analysis has permitted to propose synthetic descriptions of the problems by significantly reducing the number of governing parameters.
		• Transition between different collapse mechanisms in reinforced concrete elements This research is an extension of the research concerning the ductility in reinforced concrete structures, since it aims to analyse the competition between the shear collapse mechanism and the flexural and crushing failures already analysed with the cohesive/overlapping model. Dr. Corrado is working on the implementation of a new numerical algorithm in the framework of the Extended Finite Element Method (XFEM), to analyse a beam in its complex with generic boundary conditions and in the presence of more than one crack. The onset of fracture is modelled by means of a Mode I cohesive zone model, and the crack trajectories are evaluated step-by-step by means of the maximum hoop stress criterion. Expected results concern the prediction of the predominant collapse mechanism, the failure load as well as the analysis of the mutual transition between the different failure modes by varying the scale, the slenderness and the reinforcing steel amount. This numerical investigation is coupled to an experimental campaign carried out in the Laboratory of Materials and Structures at Politecnico di Torino. A total of 45 beams with different reinforcement percentages, sizes (scaling in the range 1:16) and slendernesses have been tested in the scheme of three-point-bending test. The results will be the basis for the validation of the proposed numerical model. This topic includes also the study of FRP strengthened beams. An analysis of the competition between different failure mechanisms, namely flexure and crushing collapse at the mid-span cross-section, and the growth of the interfacial crack, either from the edge or from the mid-span, is carried out. Applications of this research are envisaged in the design of structural strengthening.
		• Hardening cohesive zone model for metallic materials This research topic concerns the analysis of ductile fracture in metallic materials. The purpose of this research topic is to extend the cohesive zone model to metallic materials. The main novelty is the introduction of a stress vs. localized displacement law for both hardening and softening stages, on the basis of the experimental evidence that the necking phenomenon taking place in the nonlinear regime is almost scale-independent. Accordingly, the energy dissipation results to be a surface-dominated phenomenon. The hardening cohesive zone model has been implemented in a numerical algorithm, and successfully applied to describe three-point-bending tests and compact tension tests on metals. Experimental tests are carried to explore size effects on pre-notched steel beams scaled in the ratio 1:32.