Problem Set 1
Download: Problems 1.
Problem Set 2
Download: Problems 2.
Finite Automata
A simple, fragile parser for regular expressions. This produces a non-optimized, non-deterministic automata (NDFSM), in .dot format!
import sys
# a simple (but fragile) parser for regexp expressions
# to use this program: python regexp <expression> | dot -Tpdf > plot.pdf
# remember to put ( ) around kleene star expressions: (a*)b, and not a*b
free = 0;
idx = 0
def var():
global free;
free += 1;
return "g" + str(free);
def regexp(s):
global idx
print 'subgraph cluster_'+str(idx)+' {'
idx+=1
print 'label="'+s+'";'
print 'color=black;'
#trivial cases:
if len(s) == 0:
v = var()
r = (v, v, '')
print '}'
return r
if len(s) == 1 and s[0] >= 'a' and s[0] <= 'z':
r = singleton(s)
print '}'
return r
#scan for |, * and concatenation at parenthesis level 0
l = 0
for i in range(len(s)):
c = s[i]
if l == 0:
if c == "|":
r = union(regexp(s[0:i]), regexp(s[i+1:len(s)]))
print '}'
return r
if c == "*":
r = kleene(regexp(s[0:i]))
print '}'
return r
if i > 0 and ((c >= 'a' and c <= 'z') or c == '('):
r = concat(regexp(s[0:i]), regexp(s[i:len(s)]))
print '}'
return r
if c == '(':
l += 1
elif c == ')':
l -= 1
print '}'
#just remove extra parenthesis
if s[0] == '(' and s[-1] == ')':
return regexp(s[1:-1])
return None
def singleton(a):
v1, v2 = var(), var()
print v1, "->", v2, '[label="' + a + '"];'
return (v1, v2, a)
def concat(s, t):
print s[1], "->", t[0], '[label="e"];'
return (s[0], t[1], "concat("+s[2]+","+t[2]+")")
def union(s, t):
S = var();
f = var();
print S, "->", s[0], '[label="e"];'
print S, "->", t[0], '[label="e"];'
print s[1], "->", f, '[label="e"];'
print t[1], "->", f, '[label="e"];'
return (S,f,"union("+s[2]+","+t[2]+")")
def kleene(s):
v = var();
print s[1], "->", v, '[label="e"];'
print v, "->", s[0], '[label="e"];'
return (v, v, "kleene("+s[2]+")")
print "digraph {"
(s,t,e) = regexp(sys.argv[1].strip())
print t,"[shape=doublecircle];"
print s, "[style=filled];"
print >> sys.stderr, e
print "}"Using it like this:
python regexp.py 'bbb((((a*)b)|c)*)' | dot -Tpng > machine.png
writes to standard error the following:
concat(b,concat(b,concat(b,kleene(union(concat(kleene(a),b),c)))))
and produces the following image:
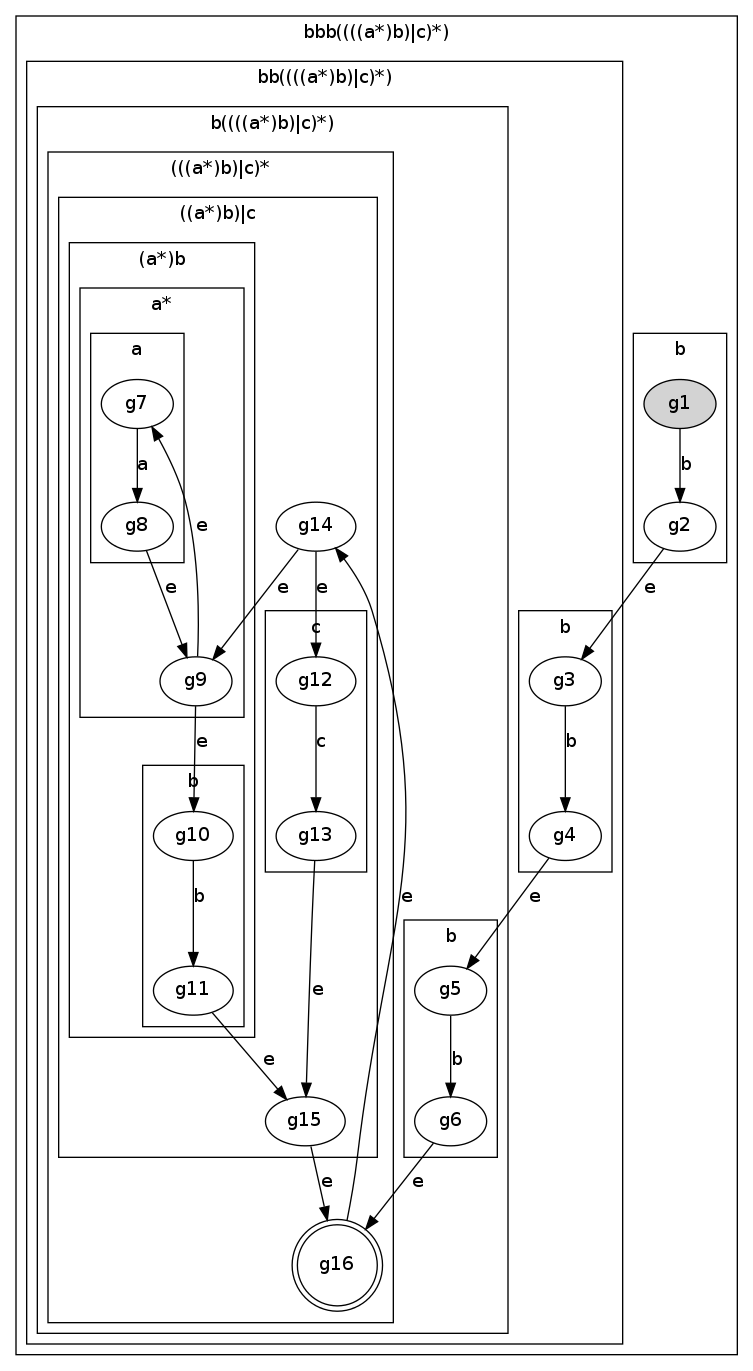 A non-deterministic finite states machine
A non-deterministic finite states machine
Download: regexp.py.
Online Book by S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani: Download