-
Usual CFD analisys tools solve a direct aerodynamic problem. The geometry of the aerodynamic surface as well as the necessary boundary are known. The flowfield is then computed numerically.
In an Inverse Problem instead, the geometry is unknown and some flow features, e.g. the pressure distributions, are prescribed at the boundary of the aerodynamic device, whose shape is then sought. From the mathematical point of view, the formulation of an inverse problem is the natural way of solving the design problem. In practice, the formulation of the inverse problem is complicated by well-posedness issues and the numerical solution often requires complex and CPU-expensive algorithms.
The approach we propose of solving aerodynamic inverse problems identifies the problem solution as the steady state of an unsteady evolution. During this transient, the flowfield tries to accommodate itself to the design data, which are prescribed as boundary conditions on the unknown surface. To do this, the surface is allowed to move. From the computational stand point, this approach requires the numerical solution of the flow governing equations on a flow domain changing in time. The algorithms for compressible and incompressible flow differ because a different numerical treatment of the flow governing equations is required. -
Inverse problems based on the incompressible Euler equations
Let us consider, for instance, the design of a stator blade. One can rely the desired performance to a certain blade load. The solution strategy is therefore to start from an initial guess of the blade geometry and to impose the desired load. For each surface element, the numerical procedure derives the wall motion that tends towards the satisfaction of the boundary conditions. The blade surface is then integrated in time, until a steady state is reached. If this happens, the geometry that realizes the desired load conditions is found.
In Figure 1 the solution process for the design of a stator blade is illustrated: to the initial guessed geometry (a) the blade load distribution is applied; since pressures in the neighbourhood of the blade is not in accord to the imposed wall pressure, blade surface start moving in order to decrease the pressure gap (b)-(c). At convergence the steady state (d) is reached. At (d) the flowfield satisfies the imposed BCs, so that the shape does not change anymore in time. The dynamics resembles the motion of a flag under the action of a constant wind.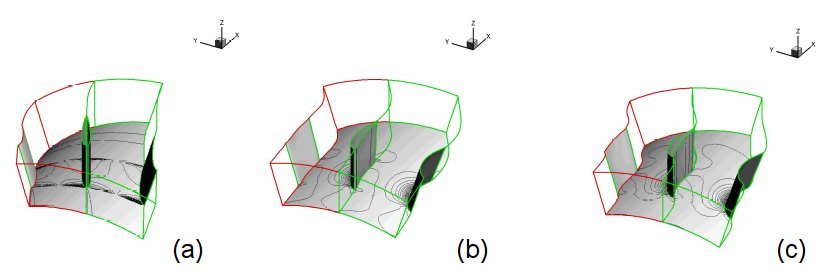
-
FIGURE 1: Solution of a 3-D inverse problem based on the Euler incompressible equations. (a) Initial guess, (b)-(c) intermediate and (d) final 3-D blade geometry and flowfield.
-
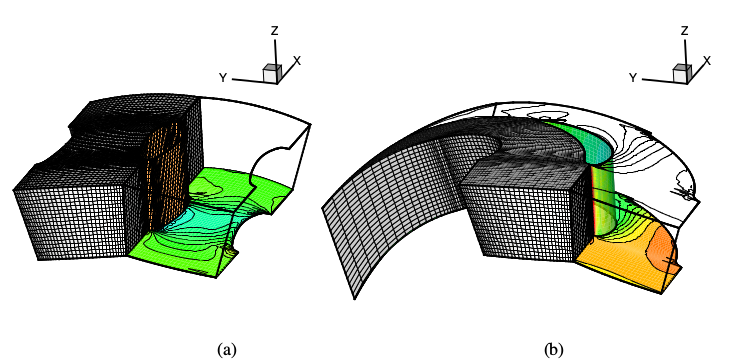
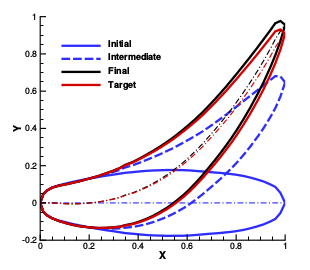
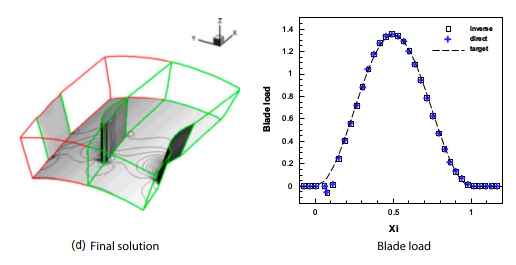
FIGURE 2: The VKI E/TU-1 Blade Test Case.
(a) Initial guess, (b) final 3-D blade geometry and flowfield. (c) Evolution of the computed blade profile at the midspan (the real geometry is also shown as "target"). -
Inverse problems based on the compressible Euler equations
Although there are substantial differences in the numerical aspects with respect to the incompressible case, the solution of the inverse problem for compressible flows follows the same footsteps.
We prefer to focus here our attention to a special application of the method. Other design problems will be shown using the full Navier-Stokes equations.
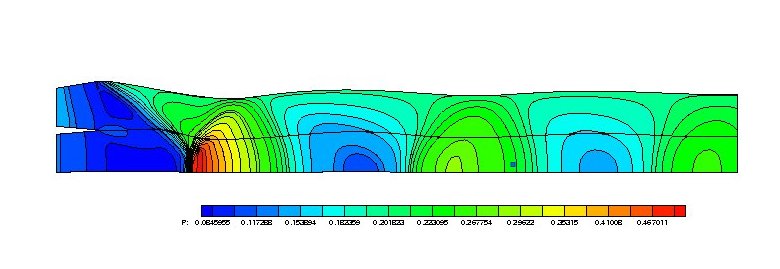
The inverse problem can be used to accurately fit fluid interfaces in supersonic flow. This becomes important, for instance, when computing the plumes of supersonic nozzles, where the out-coming flow interacts with the external flow and a very complex scenario take place. Under-resolved fluid interfaces can affect the flow pattern generated by the highly non-linear interaction between shocks, expansion waves and fluid interfaces. In Figure 3 an over-expanded two stream nozzle interacting with the external flow is shown.
-
FIGURE 3: Flow on a over-expanded two-stream nozzle interacting with the external flow.
-
Inverse Problem based on the Navier-Stokes Equation
With substantial changes, related to the different flow physics and boundary condition involved in, the above-mentioned approach to the solution of the Inverse Problem applies to the Navier-Stokes equations. In the following the inverse design of a supersonic dual-bell nozzle and of a spike nozzle are illustrated.
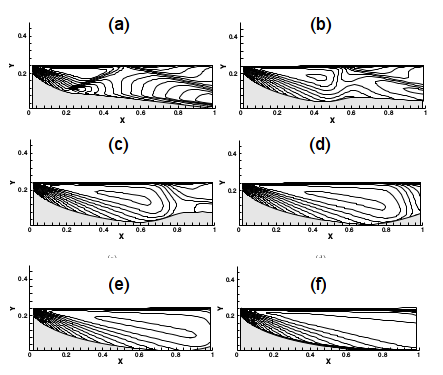
Design of a Dual-Bell Nozzle
-
FIGURE 4: Design of a Dual bell nozzle by an Inverse Method. (a) Initial guess, (b)-(c) intermediate and (d) final geometry and pressure field.
-
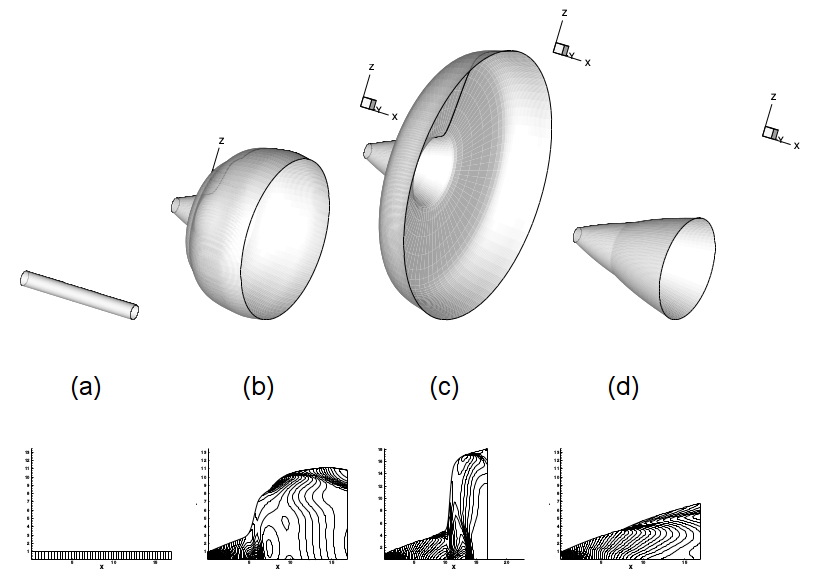
Design of a Supersonic Plug Nozzle
-
FIGURE 5: Design of a Spike nozzle by an Inverse Method. (a) Initial guess, (b)-(e) intermediate and (f) final geometry and pressure field.
-
Optimal Design
The inverse is driven by an adjoint solver in order to derive optimal design soultions
read MORE »
-
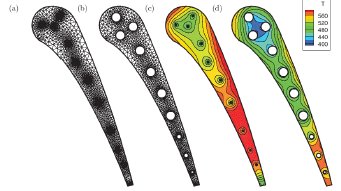
Thermal Design of Cooled Turbine Blades
read MORE »
back to RESEARCH »
Copyright @ 2015 JLab. All rights reserved.
