Predicting the past of an epidemics

Identifying the origin of an epidemic outbreak could provide invaluable information to fight the disease causing it. Unfortunately, in many cases the outbreak is not even discovered until long after the first contagion, when a large portion of the population is already infected. As an additional difficulty, most diseases spread through social channels, e.g. by proximity or sexual intercourse. While large-scale information about human contacts is becoming available, the complex topology of interactions makes well established models of diffusion in two or three dimensions inadequate. For complex contact patterns, many recent studies focus on the description of initial conditions that most likely induce severe events. However, suppose that we discover today evidence of a widespread infection; is a noisy, partial observation about the present state of the system sufficient to find the source(s)? Can we use our knowledge of the dynamics of contagion to complement or even correct our observation of the present state?

The (discrete time) SIR model works as follows. We start with a given contact graph \(G=(V,E)\), a transmission probability \(\lambda\) and a recovery probability \(\mu\). At a given time \(t\in\mathbb{N}_0\), each node \(i\) of the graph can be in one of three states (Susceptible, Infected, Recovered): \(x_i^t\in \{S,I,R\}\). Each infected node at time \(t\geq 0\) will attempt infection on susceptible neighbors independently with probability \(\lambda\) and then attempt recovery with probability \(\mu\). It is easy to see that this (Markov) process satisfies \(P(\mathbf{x}^{t+1}|\mathbf{x}^t)=\prod_i P(x_i^{t+1}|\mathbf{x}^t)\) where

\[ \begin{eqnarray*} P(x_i^{t+1}=S|\mathbf {x}^t) &=& \mathbb{I}[x_i^t=S] \prod_{j\in\partial i} (1-\lambda \mathbb{I}[x_j^t=I])\\ P(x_i^{t+1}=I|\mathbf {x}^t) &=& \mathbb{I}[x_i^t=I](1-\mu) + \mathbb{I}[x_i^t=S] (1-\prod_{j\in\partial i} (1-\lambda \mathbb{I}[x_j^t=I]))\\ P(x_i^{t+1}=R|\mathbf {x}^t) &=& \mathbb{I}[x_i^t=I]\mu + \mathbb{I}[x_i^t=R] \end{eqnarray*} \]

For a given initial condition, say one infected seed node and all other nodes in the susceptible state, this simple discrete dynamics will stochastically evolve and eventually converge (to a state with no infected nodes provided that \(\mu>0\)). An example of a possible situation at an intermediate time \(t=T\) is given by the following figure:

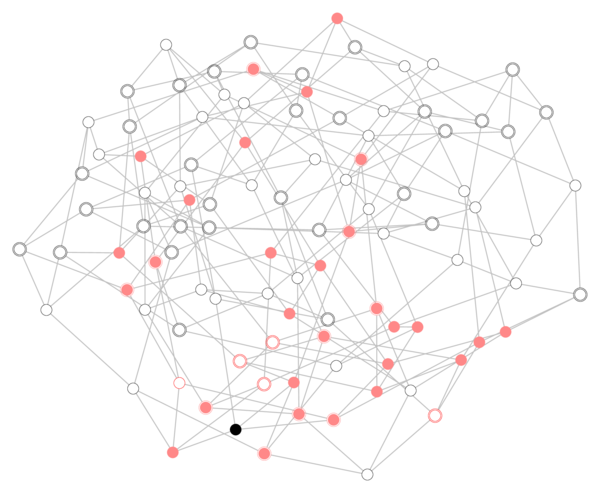
In the figure, the black node is the seed, infected nodes are given by full red circles, susceptible ones by empty black circles and recovered ones by empty red circles. Now, suppose we observe only the state of those nodes that have bolder (double) border, but we don’t kwow neither when nor where the epidemics originated. Can we guess which node was the original seed? Well, it turns out that we can! (and this particular case is actually easy)

Slides of a 2013 talk, Slides of a short 2014 talk @ Berkeley

Full description at [1; 2]

1. Altarelli, F, Braunstein, A, Dall’Asta, L, Lage-Castellanos, A, and Zecchina, R, 2014, “Bayesian Inference of Epidemics on Networks via Belief Propagation” Phys. Rev. Lett. 112(11) 118701, http://link.aps.org/doi/10.1103/PhysRevLett.112.118701.
2. Altarelli, F, Braunstein, A, Dall’Asta, L, Ingrosso, A, and Zecchina, R, 2014, “The patient-zero problem with noisy observations” Journal of Statistical Mechanics: Theory and Experiment 2014(10) P10016, http://iopscience.iop.org/1742-5468/2014/10/P10016.