The Spread Optimization problem

The k-LTM dynamics or (Bootstrap percolation dynamics) is defined as follows. At every time \(t\in\mathbb N_0\). each node \(i\) on a graph can be in one of two states \(x_i^t\in \{0,1\}\). Once a node becomes 1, it will never go back, i.e. \( x_i^{t+1}\geq x_i^t\). A node will become 1 if it has at least k neighbors that are 1. The dynamics is specified then as: \[x_i^{t+1}=\mathbb{I}(\sum_{j\in\partial i} x_j^t \geq k(1-x_i^t))\]

The following Postscript code simulates the spread dynamics on a square lattice starting by a random configuration at time 0. You can adjust the parameters by just editing the first lines of the postscript file: theta (k), n (side of the lattice), T (final time), seedprob (independent probability of being 1 at time t=0). By flipping rapidly through the 100 printed pages you would see something like this:

Postscript code:

%!PS-Adobe-3.0
%%BoundingBox: 0 0 600 600
/theta 2 def
/T 100 def
/n 100 def
/seedprob .1 def
/size 600 def
/allpages false def


/t 0 def
/c size n div def
/rand01 { rand 2147483647 div } def
 
/m { moveto } bind def
/l { rlineto} bind def


/drawspread {
        0 1 n 1 sub { /y exch def
		0 1 n 1 sub { /x exch def
			spread x get y get dup T eq { pop 0 0 0 setrgbcolor } {
				T div /dd exch def
				dd 0.2 exp 0.3 mul
				dd 0.2 exp 0.6 mul
				dd 0.9 exp
				setrgbcolor
				x c mul y c mul m
				c 0 l 0 c l c neg 0 l closepath fill
			} ifelse
		} for
        } for
	0 0 0 setrgbcolor
	n 2 div c mul n c mul 10 add m
	t 10 string cvs 
	show
} def


 
/isfinite { exch oldspread exch get exch get T lt } bind def

/inccnt { cnt 1 add /cnt exch def } bind def

/neighbors { /y exch def /x exch def /cnt 0 def
	y 1 sub /y1 exch def y1 0 ge {x y1 isfinite { inccnt } if } if
	y 1 add /y1 exch def y1 n lt {x y1 isfinite { inccnt } if } if
	x 1 sub /x1 exch def x1 0 ge {x1 y isfinite { inccnt } if } if
	x 1 add /x1 exch def x1 n lt {x1 y isfinite { inccnt } if } if
	cnt
} bind def

%% /Helvetica findfont
%% 20 scalefont setfont

/iter {
	/moved 0 def
	% copy to oldspread
	0 1 n 1 sub { /x exch def 
		oldspread x get 0 spread x get putinterval
	} for
	t 1 add /t exch def
        0 1 n 1 sub { /x exch def
        	0 1 n 1 sub { /y exch def
			oldspread x get y get T eq { 
				x y neighbors theta ge { 
					spread x get y t put 
					moved 1 add /moved exch def 
				} if
			} if
        	} for 
	} for
} bind def

/oldspread [ n {[ n {T} repeat]} repeat ] def
/spread [ n {[ n { rand01 seedprob lt {0}{T} ifelse } repeat]} repeat ] def
T 1 add { 
	drawspread showpage 
	allpages { drawspread showpage } if
	iter moved 0 eq { exit } if t = 
} repeat
drawspread showpage 
%%EOF

Warning! Real printing not advised. This code, although being less than two kilobytes long, produces T=100 pages of output! Did you know that Postscript is a real programming language? If you are as environment friendly as I am, you will save a rainforest or two by running the following command instead of printing the Postscript file:

# using Imagemagick to build an animated gif
convert spread.ps spread.gif

Of course, initial conditions need not to be random. One could seek such conditions with the smallest possible number of 1s such that the propagation still covers the full graph. Can you guess what is the optimal solution for the case above (k=2)? We investigated this issue, in order to solve the important problem of producing the following carpet designs (here k=3):

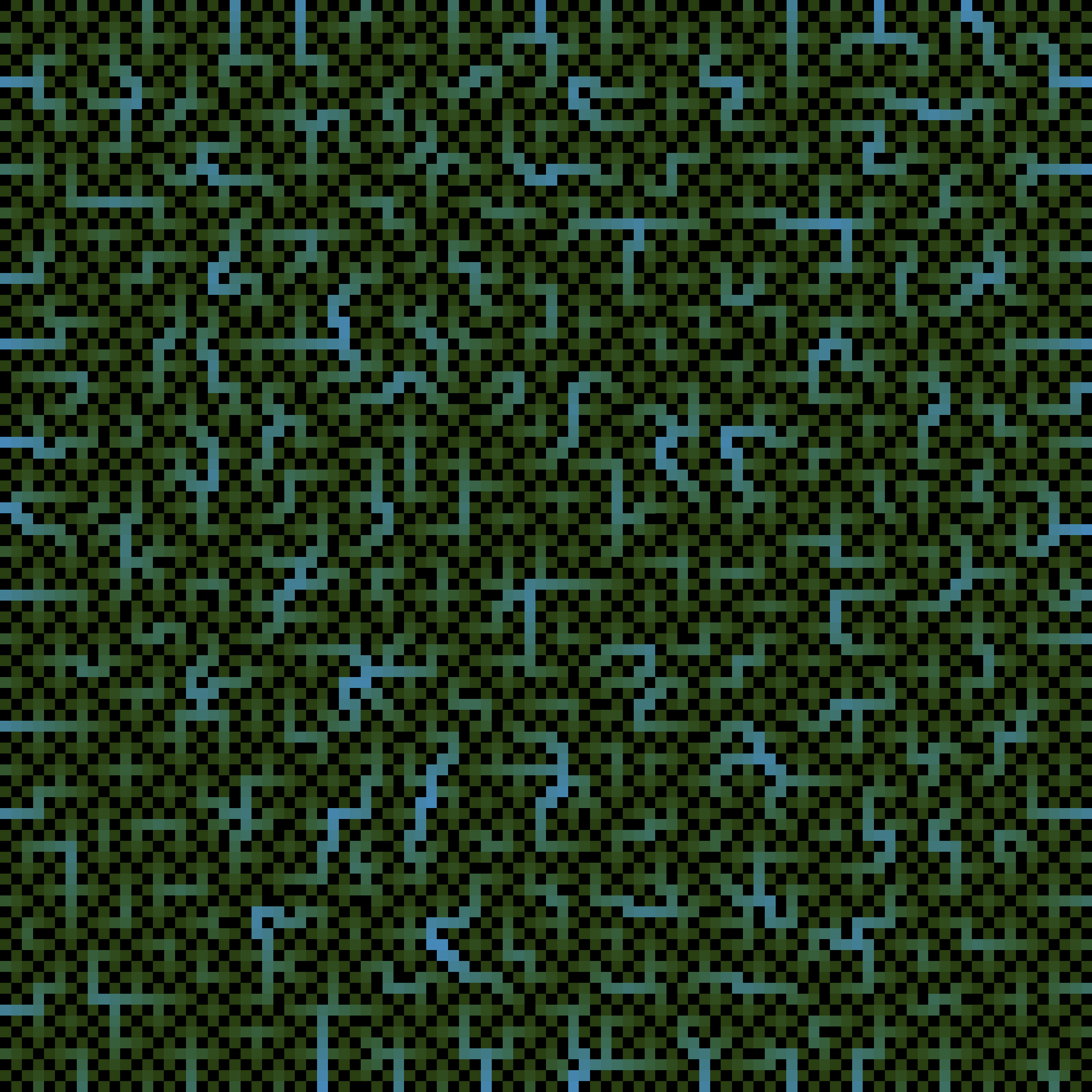
or for an hexagonal lattice (each site has six neighbors) with k=5:

See more serious results on random graphs, and an application to viral marketing: slides, [1; 2]

Altarelli, F, Braunstein, A, Dall’Asta, L, and Zecchina, R, 2013, “Optimizing spread dynamics on graphs by message passing” J. Stat. Mech. 2013(09) P09011, http://iopscience.iop.org/1742-5468/2013/09/P09011.
Altarelli, F, Braunstein, A, Dall’Asta, L, and Zecchina, R, 2013, “Large deviations of cascade processes on graphs” Phys. Rev. E 87(6) 062115, http://link.aps.org/doi/10.1103/PhysRevE.87.062115.

Alfredo Braunstein