This C++ code implements a near-capacity lossy compressor (source coding) for a random independent binary source, using special ultra-sparse LDPC codes in \(GF(2^k)\)(the Galois field of \(2^k\)elements). An example of the scheme in action is given below:
 |
 |
 |
 |
| source | compression | compressed | decompressed |
|---|
The data to be compressed is represented by the first panel (60x100 black and white image, amounting to 6000 bits). For this example, \(k=6,\) so the data is divided into \(N=1000\) chunks of 6 bits, each one corresponding to a value in \(GF(2^6)\). A specially crafted random linear system of \(N=1000\) variables and \(M=500\) equations in \(GF(2^6)\)is employed (one example system is included in the .tgz archive). The compression rate is thus fixed to \(R=M/N=0.5.\) An iterative procedure (Reinforced Belief Propagation) is run to find a solution of the linear system that is as close as possible to the initial image. During iteration, the current solution vector is shown in the second panel. Once converged, an assignement of 500 variables (information bits) suffices to index this solution (black and white pixels in the third panel). Decompression (last panel) is achieved by simply recovering this solution given the information bits (achieved by backwards substitution in the system of equations); the resulting image differs from the initial one in about 11%, i.e. has a distortion \(D\simeq 0.11.\) The compression scheme is fully described here: [1], [2]
A word of warning: to compress pictures, one can exploit characteristics of ‘normal’ real-world images (specially images of dinosaurs) and achieve better compression rates. The real power of this scheme is shown on data coming from unbiased independent bits. In this case, the theoretical limit for the distortion as a function of the compression rate is given by Shannon’s capacity curve, and our scheme is almost as good as you can get:
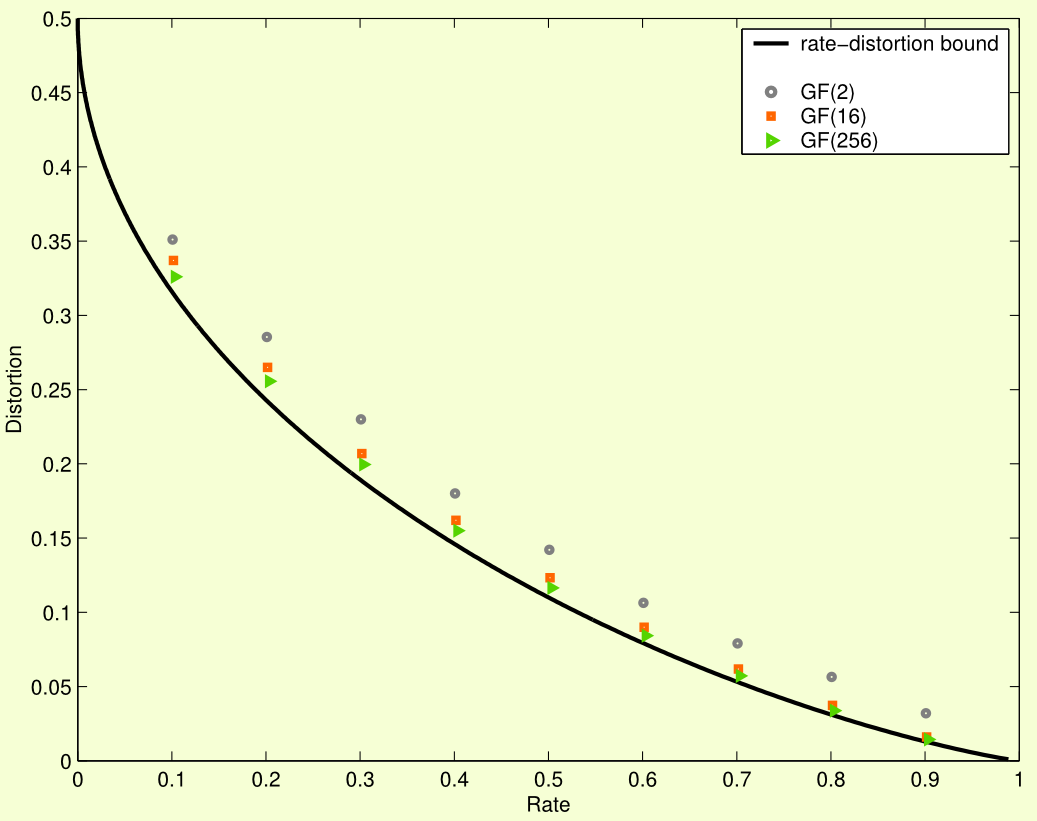
To make a 30 run compression / decompression roundtrip simulation of random 01 bits with this code, run
# We provide a 5-reduced random configurational
# model GF(Q) code in codes/ as example.
./gfrbp < codes/FG_Q64_N1000_M500_s0_r5.txtCheck out the README text file inside the .tgz archive. The original artistic image in its full glory (not for the faint of heart):

- Braunstein, A, Kayhan, F, and Zecchina, R, 2011, “Efficient data compression from statistical physics of codes over finite fields” Phys. Rev. E 84(5) 051111, http://link.aps.org/doi/10.1103/PhysRevE.84.051111.
- Braunstein, A, Kayhan, F, and Zecchina, R, 2009, “Efficient LDPC Codes over GF(q) for Lossy Data Compression,” in IEEE International Symposium on Information Theory, 2009. ISIT 2009 (Seul, Korea), http://arxiv.org/abs/0901.4467.