Alfredo Braunstein

This is the msgsteiner code for the Prize-collecting Steiner Tree Problem on graphs (PCST). The PCST is a straightforward generalization of the famous Steiner Tree Problem on Graphs, which simply put, asks to find the cheapest way to connect a subset of nodes on a graph. Precisely, the PCST problem is defined as follows: given a graph \(G=(V,E)\), a link cost function \(\omega:E\to\mathbb R_{>0}\) and a node prize function \(p:V\to \mathbb R\), find the tree \(T=(V_T,E_T)\) minimizing

\[H(T)=\sum_{e\in E_T} \omega(e) - \sum_{i\in V_T} p(i).\]

The Minimum Steiner Tree problem [1] can be seen as a particular case in which for a set \(K\) called terminals, \(p(i)=L, i\in K\), \(p(i)=0, i\notin K\) for a large enough constant \(L\). It is NP-Hard. For \(K=V\), the problem becomes the standard (and polynomial) Minimum Spanning Tree problem. In this limit, it can be proved that the message-passing equations are exact [2].

We studied an “arborescent” variant of the PCST problem: a “root” node and a bound to the maximum distance \(D\) from any node in the tree to the root are also given as inputs. For finite \(D\), even the spanning tree version (with all nodes as terminals) is NP-Hard! Nevertheless, Max-Sum (the T=0 version of Belief Propagation) seems to give an excellent heuristics on random and benchmark instances.

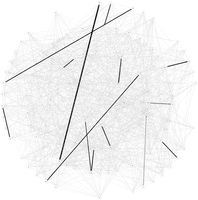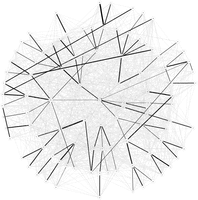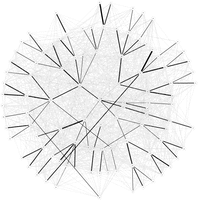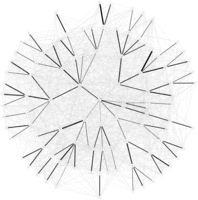Max-Sum on the `\(D=4\)` Arborescent Minimum Spanning Tree

./msgsteiner --help
Usage: ./msgsteiner <option> ... 
	where <option> is one or more of:
	--help                                produce help message
	-o [ --tree ]                         outputs final tree to std output
	-M [ --messages ]                     output messages on convergence
	-j [ --threads ] arg                  sets number of threads
	-s [ --seed ] arg                     sets instance seed
	-z [ --mseed ] arg                    sets messages seed
	-d [ --depth ] arg (=10)              set maximum depth
	-t [ --maxit ] arg (=100000)          set maximum number of iterations
	-e [ --tolerance ] arg (=1.0000000000000001e-05) 
	                                      set convergence tolerance
	-r [ --noise ] arg (=9.9999999999999995e-07) 
	                                      set random factor
	-g [ --rein ] arg (=0)                sets reinforcement parameter rein
	-y [ --decision ] arg (=10)           program converges after this 
	                                      repeats of the decision variables

Check out the README text file inside the .tgz archive.

The PCST problem (and this algorithm) can be used to unveil hidden functional networks in the context of cell signaling [3].

More about the PCST: [4] [5], PSB’14

1. Bayati, M, Borgs, C, Braunstein, A, Chayes, J, Ramezanpour, A, and Zecchina, R, 2008, “Statistical Mechanics of Steiner Trees” Phys. Rev. Lett. 101(3) 037208, http://link.aps.org/doi/10.1103/PhysRevLett.101.037208.
2. Bayati, M, Braunstein, A, and Zecchina, R, 2008, “A rigorous analysis of the cavity equations for the minimum spanning tree” Journal of Mathematical Physics 49(12) 125206, http://link.aip.org/link/?JMP/49/125206/1.
3. Bailly-Bechet, M, Borgs, C, Braunstein, A, Chayes, J, Dagkessamanskaia, A, François, J-M, and Zecchina, R, 2011, “Finding undetected protein associations in cell signaling by belief propagation” PNAS 108(2) 882–887, http://www.pnas.org/content/108/2/882.
4. Biazzo, I, Braunstein, A, and Zecchina, R, 2012, “Performance of a cavity-method-based algorithm for the prize-collecting Steiner tree problem on graphs” Phys. Rev. E 86 026706, http://link.aps.org/doi/10.1103/PhysRevE.86.026706.
5. Tuncbag, N, Braunstein, A, Pagnani, A, Huang, S-S C, Chayes, J, Borgs, C, Zecchina, R, and Fraenkel, E, 2012, “Simultaneous Reconstruction of Multiple Signaling Pathways via the Prize-Collecting Steiner Forest Problem,” in Research in Computational Molecular Biology Ed B Chor Lecture Notes in Computer Science (Springer Berlin Heidelberg), pp 287–301, http://dx.doi.org/10.1007/978-3-642-29627-7_31.